展開公式
1 \( (x+a)(x+b)=x^2+(a+b)x+ab \)
| (1) | $$ (x+3)(x+5) $$ この式を計算(展開)する。括弧の中を項に分けたとき |
| (2) | $$ ({\color{red}x}\ \vdots+3)({\color{red}x}\ \vdots+5) $$ 左右の括弧の中に同じ項が含まれるならば(この式では\({\color{red}x}\) という項) |
| (3) | $$ (x\ \vdots+3)(x\ \vdots+5)=x^2+5x+3x+15 $$ 漏れなく掛け合わせると |
| (4) | $$ (x\ \vdots+3)(x\ \vdots+5)=x^2\ \vdots {\color{red}+5x}\ \vdots {\color{red}+3x}\ \vdots+15 $$ というように同類項(文字部分が同じ項)ができる。同類項は計算できるので、 |
| (5) | $$ (x\ \vdots+3)(x\ \vdots+5)=x^2\ \vdots \color{red}+8x\ \color{black}\vdots+15 $$ と計算しておく必要がある(\(x\) が5個と\(x\) が3個なので、あわせて8個) |
| (6) | これを一発で処理しようというのが冒頭の展開公式。\(x\) の係数は足すだけで、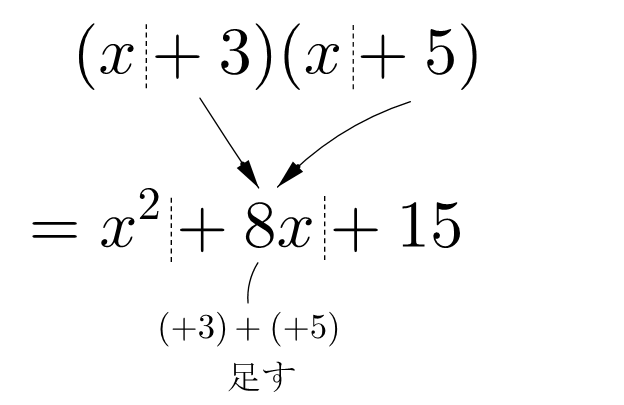 |
| (7) | 数の項は掛けるだけで求められる |
| (8) | 足してなんぼ、掛けてなんぼと覚えて使うと便利 |
| (9) | 例えば\((x-3)(x-5)\) ならば、 |
| (10) | \((x \vdots {\color{red}-3})(x \vdots {\color{red}-5})\) なので、足して\(-8\)、掛けて\(+15\)。 したがって \((x-3)(x-5) = x^2-8x+15\) |
| (11) | 例えば\((x+3)(x-5)\) ならば、 |
| (12) | \((x \vdots {\color{red}+3})(x \vdots {\color{red}-5})\) なので、足して\(-2\)、掛けて\(-15\)。 したがって \((x+3)(x-5) = x^2-2x-15\) と、簡単に展開できる |