展開公式
2\( (a+b)^2=a^2+2ab+b^2 \)
\( (a-b)^2=a^2-2ab+b^2 \)
| (1) | $$ (a+b)^2 $$ この式を計算(展開)する。2乗は同じものを2回掛けることなので |
| (2) | $$ (a+b)(a+b) $$ を計算(展開)するのと同じ。括弧の中を項に分け、漏れなく全部掛けると |
| (3) | ②と③で同じものができる。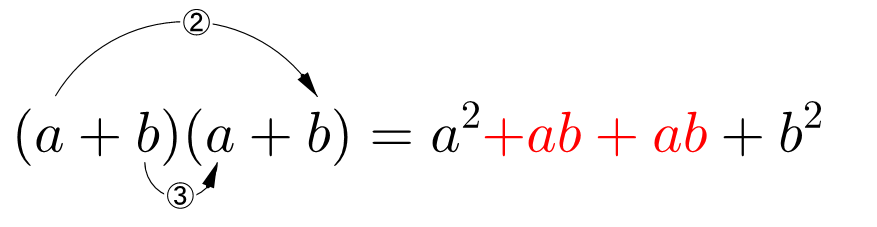 |
| (4) | 元の式でいうと、括弧の中の2つの項(\(a\) と\(+b\))を掛けたものが2個できるということ。 $$ (a\ \vdots +b)^2=a^2+ab{\color{red}\times 2}+b^2$$ |
| (5) | \((a+b)^2=a^2+b^2\) だと勘違いする人が多いので、 |
| (6) |
2乗の展開は
|
| (7) | たとえば\((x\ \vdots +2)^2\) なら、おまけは\(x \times (+2)=+2x\)。その2倍は\((+2x)\times 2=+4x\)。 したがって \((x+2)^2=x^2+4x+4\) |
| (8) | \((x\ \vdots-3)^2\) なら、おまけは\(x \times (-3)=-3x\)。その2倍は\((-3x)\times 2=-6x\)。 したがって \((x-3)^2 =x^2-6x+9\) |
| (9) | 2乗の展開は、おまけは2倍を忘れずに。 |